Brøker

Brøkdele
Ark der viser en opdeling i brøkdele, download pdf-fil.

Diverse ark til download.

• Et dokument, der gennemgår regnereglerne for brøkerne med eksempler. Download pdf-fil (6 sider). 
• Et dokument, der lidt kortere gennemgår brøkregnereglerne. Download pdf-fil (3 sider).
• Et ark, der viser hvordan et blandet tal ændres til en uægte brøk. Download pdf-fil.

Herunder er der en sammenfatning af pdf-filerne.

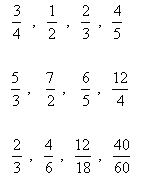
En ægte brøk har en tæller der er mindre end nævneren. Værdien af en ægte brøk er mellem 0 og 1.

En uægte brøk er en brøk, hvor tælleren er større end nævneren. Værdien af en uægte brøk er større end 1. En uægte brøk kan forkortes til et blandet tal.

Brøker med samme værdi


Fx
At forlænge og forkorte brøker

• at forlænge en brøk = En brøk forlænges ved at gange tæller og nævner med samme tal
• at forkorte en brøk = En brøk forkortes ved at dividere tæller og nævner med samme tal

Den kan også forståes således at et tal ikke ændrer værdi når den ganges med tallet 1. Det kan vises ved at gange med et stort 1-tal, der repræsenterer en brøk, fx 4/4.

Dvs. brøken 3/5 ganges med 4/4 for at få tælleren til 20. Derved forlænges brøken til 12/20 vha. et stort 1-tal.

Den følgende illustration viser at du i 1-tallet kan indsætte enhver tænkelig brøk, når bare den har samme værdi i tæller og nævner. Dvs. har værdien 1.

I eksemplet skal du finde ud af hvad der skal skrives i brøkens nævner. Hvad mener du der skal stå?

Fællesnævner = når flere brøker har det samme tal til at stå i nævneren.

Addition og subtraktion

• Når brøker skal adderes (lægges sammen) eller subtraheres (trækkes fra hinanden), skal de have en fælles nævner

eksempel
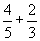Fællesnævneren findes ved at gange de to nævnere med hinanden. Her ganges 5 med 3 og det giver en fællesnævner på 15.
15 deles nu med nævneren fra hver brøk og resultatet ganges med tælleren. Her deles 15 med 5 og resultatet 5 ganges med 4. Resultatet af denne giver 12. Således er den ene brøk blevet forlænget til 15'ende-dele. Se herunder.

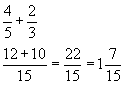
• 5 går op i 15 tre gange. 3 går op i 15 fem gange.
• Gang tælleren i den første brøk (4) med tre for at få 12.
• Gang tælleren i den anden brøk (2) med fem for at få 10.
• Skriv de to resultater over brøkstregen og læg sammen.

Multiplikation

• at gange en brøk med et helt tal = "Gange i tælleren og beholde nævneren" eller a/b × c
• at gange brøker med hinanden = Brøker ganges med hinanden ved at gange tæller med tæller og nævner med nævner

Division

• at dividere en brøk med et helt tal = En brøk divideres med et tal ved at gange nævneren med tallet
• at dividere med en brøk = "Gange med den omvendte brøk" eller a : b/c = a × c/b

---

Brøkers fortegn

• Hvis tæller og nævner har samme fortegn, er brøken positiv.
• Hvis tæller og nævner har forskellig fortegn, er brøken negativ.

Andre regler

• En nævner må aldrig være nul.
• Et helt tal kan opfattes som en brøk med nævneren 1 (f.eks. 3 = 3/1).
• Er tæller og nævner lige store (16/16), er brøken lig med 1 (uegentlige brøker).
• Forekommer der brøker i en brøks tæller og nævner, taler man om brøks brøk eller bruden brøk.
• 2 brøker, hvis produkt er 1, kaldes reciprokke.